EchoSun's Blog

Life is short, knowledge transfer.

0%

机器视觉

发表于 更新于 分类于 阅读次数：
本文字数： 3.5k 阅读时长 ≈ 3 分钟
机器视觉入门随笔。

机器视觉

方法主要是用深度学习的方法——师哥

概论

方向有图像分类，目标检测，语义分割，实例分割，视频追踪等——师哥

基本CNN网络

如果想做计算机视觉的话就按照这个流程学，先看一些基本的CNN网络，比如AlexNet，ResNet等，然后再做一些YOLO、RCNN、SSD这些更高级的框架——师哥

MPL 多层感知机

以 MPL为例，学习梯度下降法、链式求导法则和神经网络的基本结构原理。

Youtube: 3Blue1Brown视频课

MPL结构图

MPL结构图

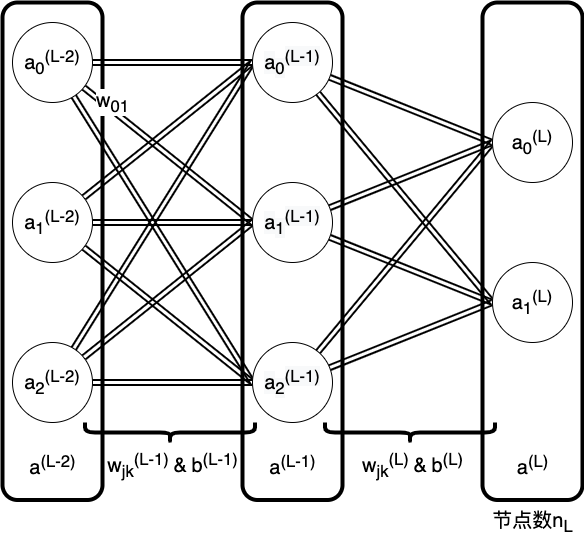
MPL变量关系图图

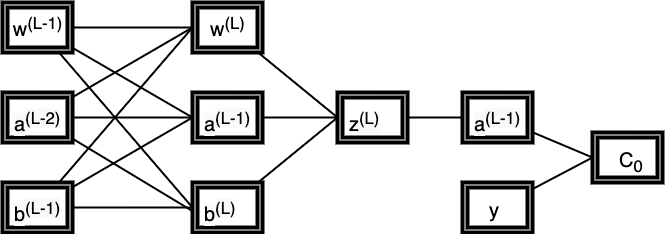
MPL结构图

MPL中链式求导法则

数学符号及对应公式的定义：

  • 误差$C = \sum_{j=0}^{n_L-1} (a_j^{(L)}-y_j)^2$
  • 各神经元的中间变量$z_j^{(L)}=w_{kj}^{(L)}a_k^{(L-1)}+b_{k}^{(L)}$ ，其中，L代表层数，b代表偏置
  • 进过激活函数后，各神经元的输出 $a_j^{(L)}=\sigma(z_j^{(L)})$

根据上述定义，可以写出链式求导公式：
$$
\frac{\partial C}{\partial w_{kj}^{(L)}} =\sum_{j=0}^{n_L-1} \frac{\partial z_j^{(L)}}{\partial w_{kj}^{(L)}} \frac{\partial a_j^{(L)}}{\partial z_j^{(L)}} \frac{\partial C_0}{\partial a_j^{(L)}} \

\frac{\partial C}{\partial b_k^{(L)}} =\sum_{j=0}^{n_L-1} \frac{\partial z_j^{(L)}}{\partial b_k^{(L)}} \frac{\partial a_j^{(L)}}{\partial z_j^{(L)}} \frac{\partial C_0}{\partial a_j^{(L)}} \

\frac{\partial C}{\partial a_k^{(L-1)}} = \sum_{j=0}^{n_L-1} \frac{\partial z_j^{(L)}}{\partial a_k^{(L-1)}} \frac{\partial a_j^{(L)}}{\partial z_j^{(L)}} \frac{\partial C_0}{\partial a_j^{(L)}}
$$

带入符号对应的公式，可以求得：
$$
\frac{\partial C}{\partial w_{kj}^{(L)}} =\sum_{j=0}^{n_L-1} a_k^{(L-1)}.\sigma^{‘}(z_j^{(L)}).2(a_j^{(L)}-y_j) \
\frac{\partial C}{\partial b_j^{(L)}} =\sum_{j=0}^{n_L-1} 1.\sigma^{‘}(z_j^{(L)}).2(a_j^{(L)}-y) \
\frac{\partial C}{\partial a_k^{(L-1)}} = \sum_{j=0}^{n_L-1} w_{kj}^{(L)}.\sigma^{‘}(z_j^{(L)}).2(a_j^{(L)}-y) \
$$

CNN

发展

上世纪 60 年代左右的神经科学中， 加拿大神经科学家David H. Hubel和Torsten Wiesel 于 1959 年提出猫的初级视皮层中单个神经元的“感受野”（receptive field）概念。

1980年，日本科学家福岛邦彦 Kunihiko Fukushima 模拟生物视觉系统，提出一种层级化的多层人工神经网络，提出的两种重要的组成单元S型细胞（S-cells）和C型细胞（C-cells）成为现在神经网络卷基层和汇合层的雏形。

卷积层用于抽取局部特征，汇合层用于抽象和容错。

Yann LeCun等人在1998年提出基于梯度学习的卷积神经网络算法LeNet，对手写数字字符的识别错误率低于1% ，成功应用于美国的邮政系统。

2012年Geoffrey E. Hinton使用Alex-Net（深度卷积神经网络）在ImageNet图像分类竞赛中表现出极好的分类准确度。开启了计算机视觉领域中深度学习的时代。

2015年，改进了卷积神经网路噢中的激活函数后，卷积神经网络在Image Net 数据机上的性能第一次超过人类预测错误率。

激活函数Activation function

  • Sigmoid函数

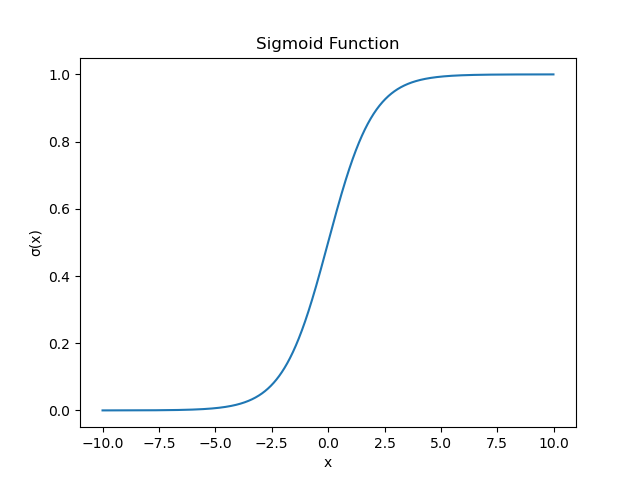    image-20211012160929883 $$ \sigma(x)= \frac{1}{1+e^{-x}} $$ Sigmoid函数求导 $$ \begin{align*} \sigma^{'}(x)&= (\frac{1}{1+e^{-x}})^{'} \\ &= [(1+e^{-x})^{-1}]^{'} \\ &= (-1).[(1+e^{-x})^{-2}]^{'}.e^{-x}.(-1) \\ &= \frac{e^{-x}}{(1+e^{-x})^2} \\ &= \frac{(1+e^{-x})-1}{(1+e^{-x})^2} \\ &= \frac{1}{1+e^{-x}} - \frac{1}{(1+e^{-x})^2} \\ &= \frac{1}{1+e^{-x}} ( 1 - \frac{1}{1+e^{-x}} ) \\ &= \sigma(x)(1-\sigma(x)) \end{align*} $$

  • ReLU函数

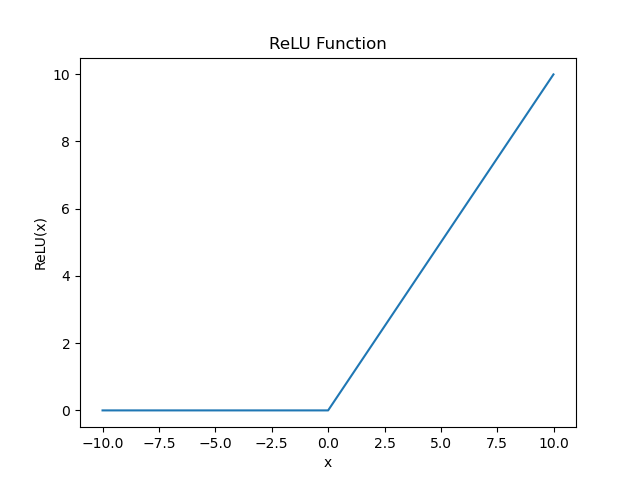    image-20211013081102280 $$ ReLU(x)= \left\{ \begin{array}{**lr**} x, x>0& \\ 0, x\leq0& \end{array} \right. $$

梯度下降

  • 梯度下降算法

    根据损失函数计算得到误差，再计算损失函数对各个参数的导数，梯度下降算法就是沿着梯度的反方向移动一段步长，从而减小误差。

    这种方法容易落到局部最优。且计算量较大，速度慢。

  • 随机梯度下降算法

    取一组minibatch，然后计算得到这一组的梯度，然后沿梯度方向下降。虽然下降的方向可能不够理想，但是计算量降低且计算速度加快。

卷积核

各向同性微分算子是拉普拉斯算子。

核心思想

卷积神经网络处理图像的核心思路：提供给计算机某一图像数组后，使计算机能输出描述该图像属于某一特定分类的概率的数字。

假设手电筒光可以覆盖 5 x 5 的区域，想象一下手电筒光照过输入图像的所有区域。在机器学习术语中，这束手电筒被叫做过滤器（filter，有时候也被称为神经元（neuron）或核（kernel）），被照过的区域被称为感受野（receptive field）。过滤器同样也是一个数组（其中的数字被称作权重或参数）

  1. 前馈运算（feed- forward 预测和推理）将高层语义信息逐层从原始数据的输入层中逐层抽象出来。
  • 卷积
  • 汇合
  • 非线性激活函数
  1. 反馈运算（训练和学习）通过最后一层，将目标任务转化为目标函数，最后通过预测值与真实值之间的损失或误差，通过反向传播算法由最后一层逐层向前反馈，从而更新每一层的参数。

接着重复前馈运算和反向传播算法，直到网络模型收敛，从而达到模型训练的目的。

使用0填充边界

使用0填充边界有以下好处：

（1）卷积了上一层之后的CONV层，没有缩小高度和宽度。 这对于建立更深的网络非常重要，否则在更深层时，高度/宽度会缩小。 一个重要的例子是“same”卷积，其中高度/宽度在卷积完一层之后会被完全保留。

（2）它可以帮助我们在图像边界保留更多信息。在没有填充的情况下，卷积过程中图像边缘的极少数值会受到过滤器的影响从而导致信息丢失。

正则化

使用正则化来解决过拟合问题。

正则化在损失函数中引入模型复杂度指标，利用给W加权值，弱化了训练数据中的噪声。

L1正则化

直接在原来的损失函数基础上加上权重参数的绝对值。假设待正则的网络层参数为w，L1正则化为：

$L = E_{in}+\lambda\sum_{j}|w_j|$

L1正则化除了同L2正则化一样能约束参数量级外，L1正则化还可以使得参数更稀疏，使得优化后的参数的一部分为0，另一部分为非0实值。

L2正则化

直接在原来的损失函数基础上加上权重参数的平方和。假设待正则的网络层参数为w，l2正则化形式为：

$L=E_{in}+\lambda\sum_{j}w_j^2$

其中，Ein 是未包含正则化项的训练样本误差，λ控制正则项大小，较大的λ取值将较大程度约束模型复杂度；反之亦然。实际使用时，一般将正则项加入目标函数（损失函数），通过整体目标函数的误差反向传播，从而达到正则项影响和指导网络训练的目的。

L2正则化在深度学习中有一个常用的叫法是“权重衰减”，另外L2正则化在机器学习中还被称为“岭回归”或Tikhonov正则化。

具体步骤

  1. 使用0填充边界
  2. 卷积
  3. 池化
    1. 实现了两种池化方法：最大池化和平均池化

多模态

多模态